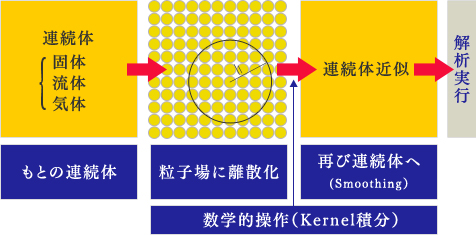
SPH 粒子法は、FEM における要素やFDM における格子を必要としない メッシュフリー解析手法です。
もとの連続体を離散化し、粒子、すなわち質量と寸法を有する微小物質素片の集合体とみなすとともに、もとの連続体に加わる力や熱的変化を、粒子間に働く力の相互作用や熱伝導として捉えます。着目する粒子（評価点）の挙動を、影響半径の中の他の粒子の物理量で面補間／球補間するという数学的操作（Kernel 積分*）を施した上で、最終的には、再び連続体近似（ Smoothing ）することによって、連続体の変形や応力分布、熱伝導等をシミュレート（解析）します。

＊Kernel 関数（重み関数）を用いた物理量の補間

FEM やFDM で用いる、格子を空間に固定する オイラー的手法は、流体解析などの広域な運動を取り扱う解析には適していますが、連続体を構成する各部位の履歴を追跡できないこと、また移流項の精度確保が困難であるといった問題があります。
SPH粒子法は、連続体上の各部分を時間的に追跡する ラグランジュ的手法を用いて連続体のさまざまな運動を記述することによって、上記のような問題点を補い得る優れた解析技術です。